Academic example of Machine Learning
Use case

Our purpose here is to show an academic Machine Learning on a Lorentz cloud. First, let’s generate 1 million of 3D points by using

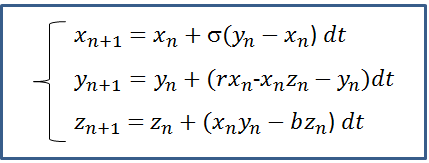
with x0=12, u0=13, z0=5, σ=10, r=30, b=3 and dt=0.001.

Then, let randomly select 300 000 points… and forget the above coordinate formulae ! Can we train a neural system in order to obtain z from x and y values ? The answer is obviously yes !
We will process the training on the 300 000 points (the training set) and assess the performance on the remaining ones (the validation set).
With NEHOOV, this is straighforward : we give training & validation sets, then we launch the meta-algorithm with one clic ! Neural models are then build, until the discovery of an ‘optimal’ one. Below are given some illustrations (we do not give the number of hidden layers) :

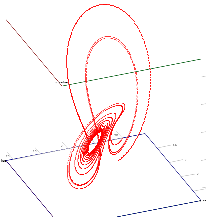	Initial Lorentz cloud (training + validation)
	One (randmoly choosen) neural network of architecture (X,Y)540Z, with sigmoïd and linear activation functions :
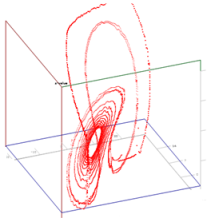	Another (randmoly choosen) neural network, of architecture X,Y)8170Z, with sigmoïd, linear, sinus anf exponential activation functions :

We clear see that a neural network with ~200 neurons & using several activation functions replicate very well our Lorentz cloud !